Arxiv
Code
Video
*equal contribution
Code is released.
3D Convex Splatting achieves high-quality novel view synthesis and fast rendering by representing scenes with 3D smooth convexes. In contrast, the softness of Gaussian primitives often results in blurring and loss of detail, while 3D Convex Splatting effectively captures sharp edges and fine details.
Recent advances in radiance field reconstruction, such as 3D Gaussian Splatting (3DGS), have achieved high-quality novel view synthesis and fast rendering by representing scenes with compositions of Gaussian primitives. However, 3D Gaussians present several limitations for scene reconstruction. Accurately capturing hard edges is challenging without significantly increasing the number of Gaussians, creating a large memory footprint. Moreover, they struggle to represent flat surfaces, as they are diffused in space. Without hand-crafted regularizers, they tend to disperse irregularly around the actual surface.
To circumvent these issues, we introduce a novel method, named 3D Convex Splatting (3DCS), which leverages 3D smooth convexes as primitives for modeling geometrically-meaningful radiance fields from multi-view images. Smooth convex shapes offer greater flexibility than Gaussians, allowing for a better representation of 3D scenes with hard edges and dense volumes using fewer primitives. Powered by our efficient CUDA-based rasterizer, 3DCS achieves superior performance over 3DGS on benchmarks such as Mip-NeRF360, Tanks and Temples, and Deep Blending. Specifically, our method attains an improvement of up to 0.81 in PSNR and 0.026 in LPIPS compared to 3DGS while maintaining high rendering speeds and reducing the number of required primitives. Our results highlight the potential of 3D Convex Splatting to become the new standard for high-quality scene reconstruction and novel view synthesis.
The 3D smooth convex is represented with a point set that is projected in the 2D camera plane. We extract the line-delimited convex hull of the projected points and define the signed distance function for each line. The lines are combined to define an indicator function for each pixel based on smoothness δ and sharpness σ of the 3D convex. The pipeline is differentiable end-to-end, which allows the parameters of the smooth convex primitives to be optimized based on the rendered images.
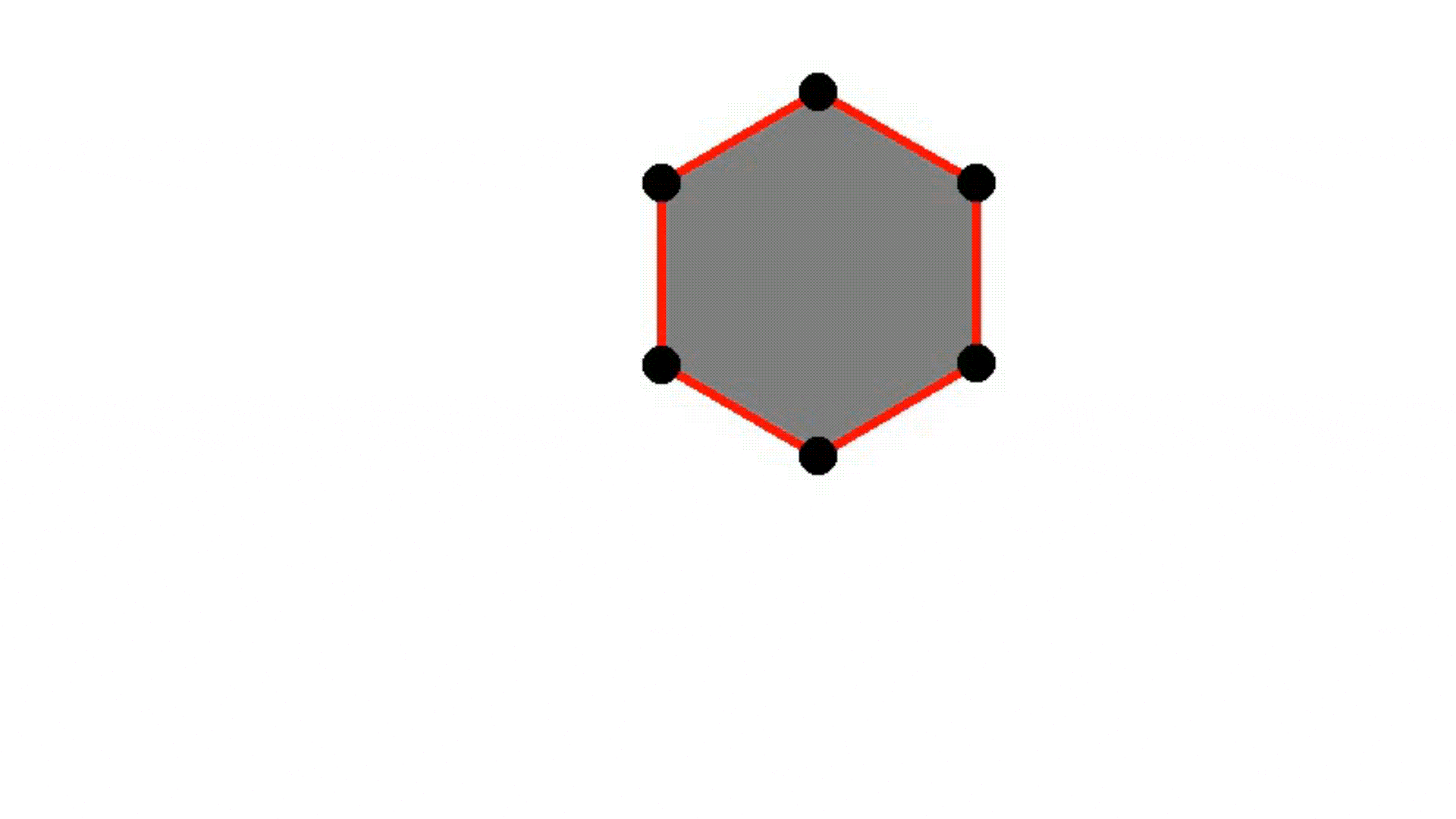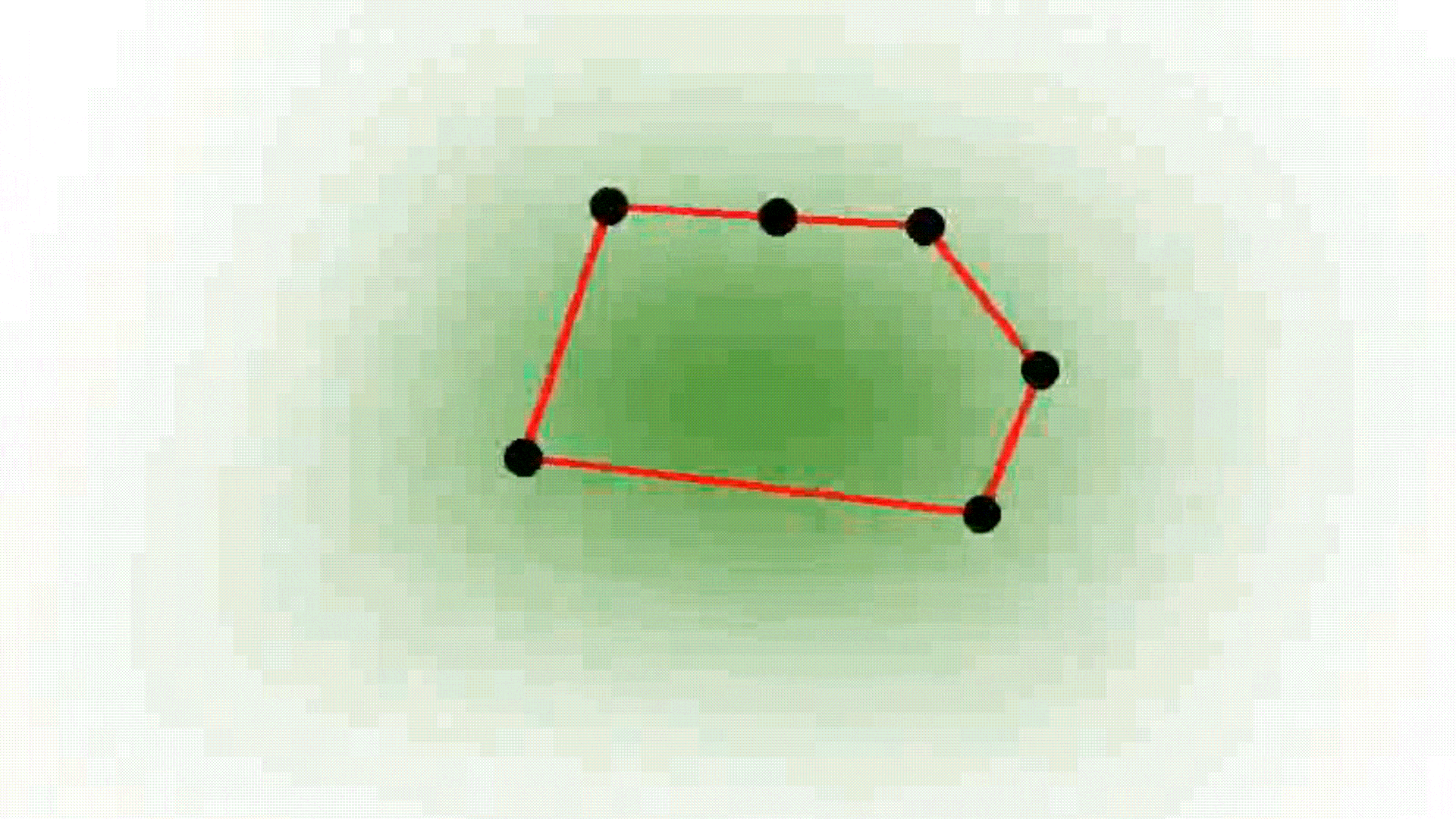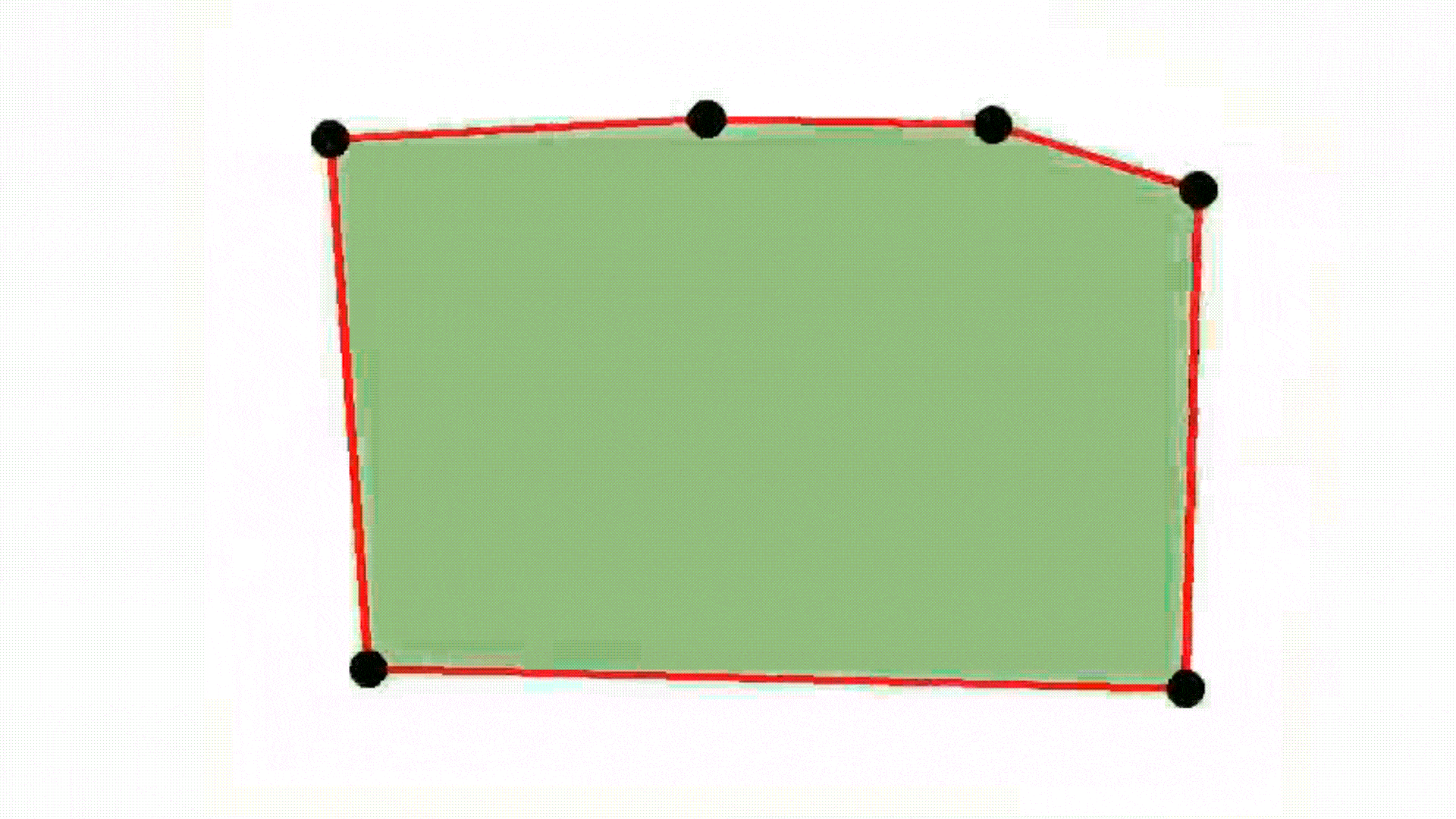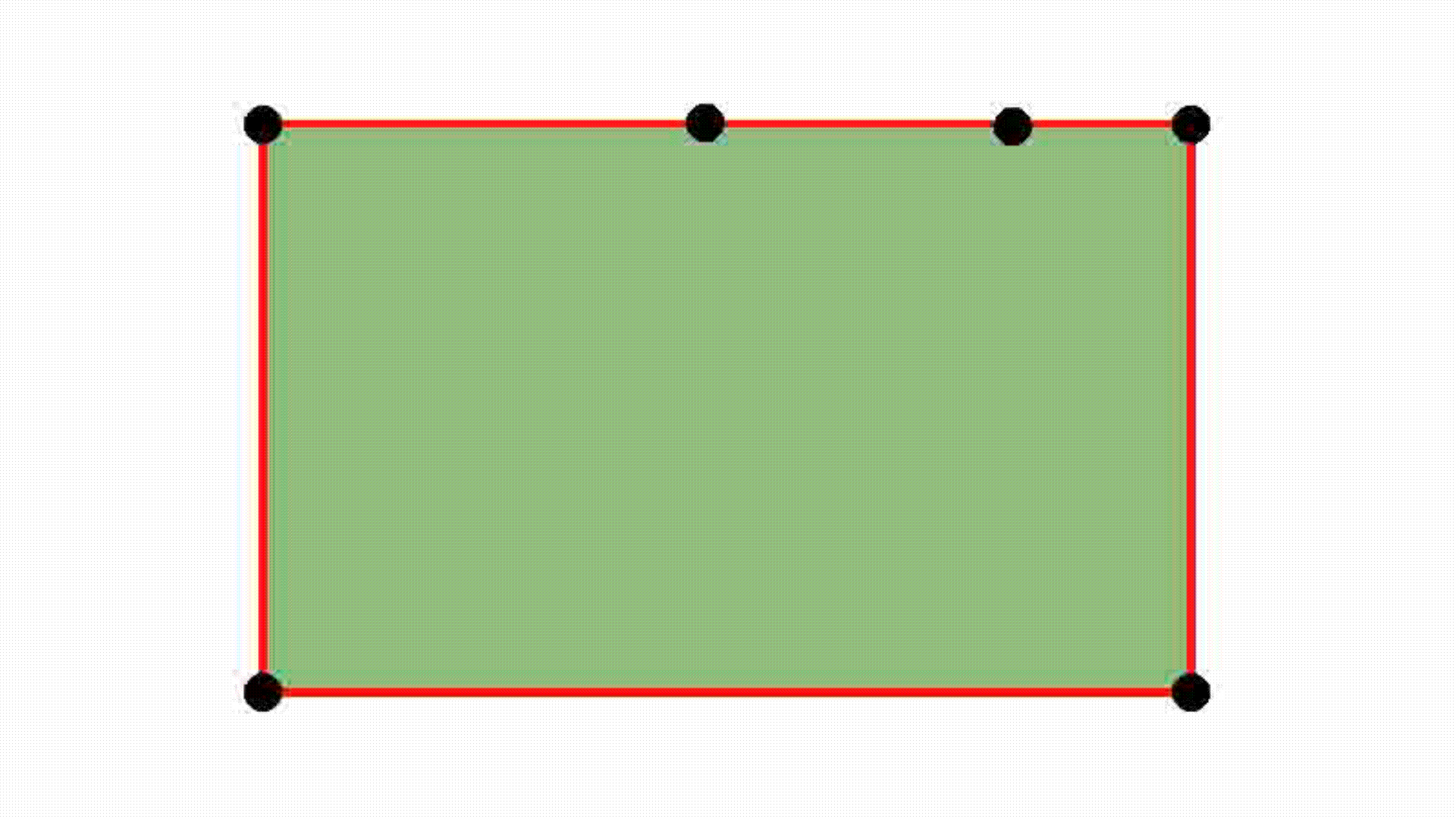
Rectangle
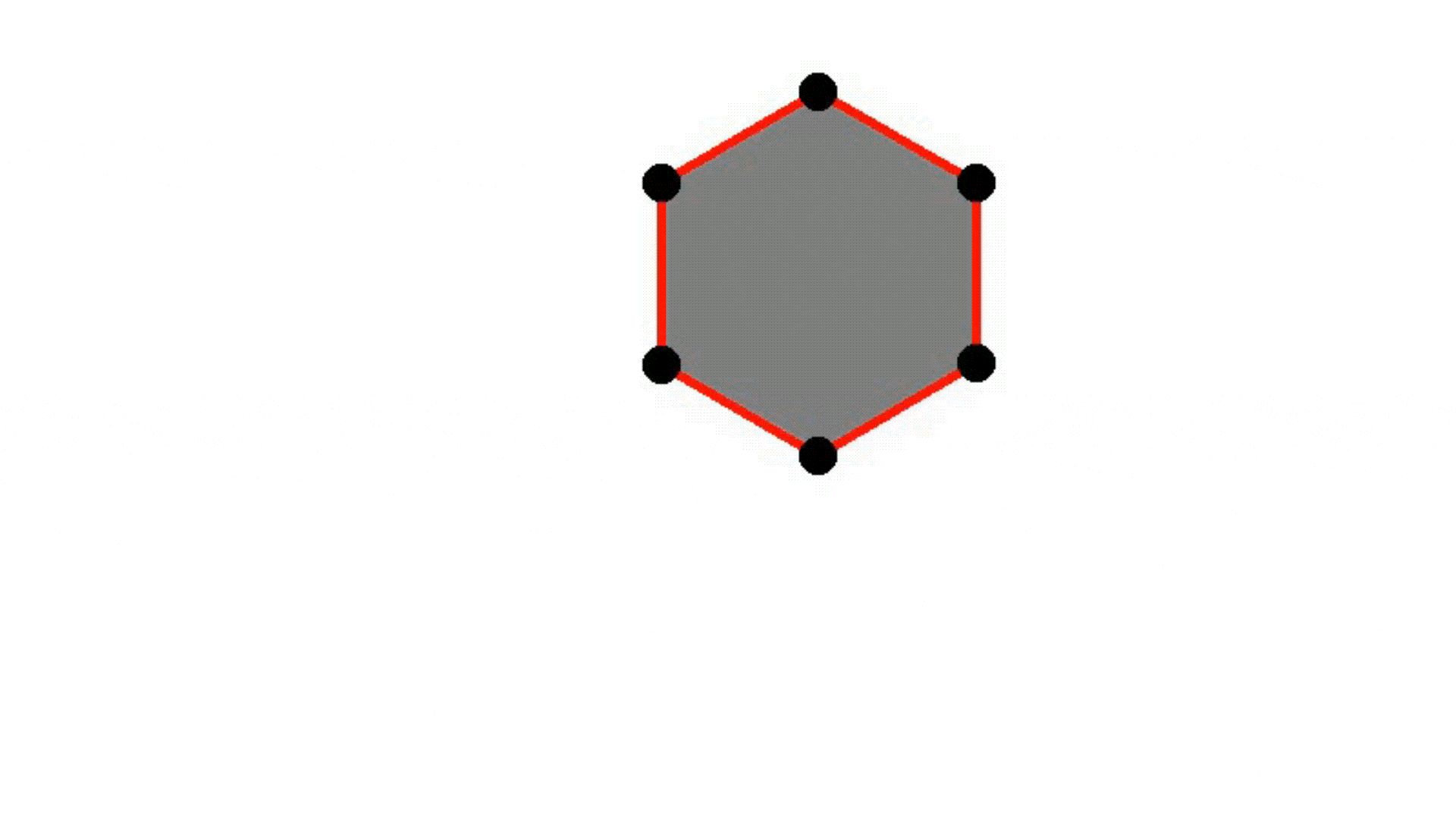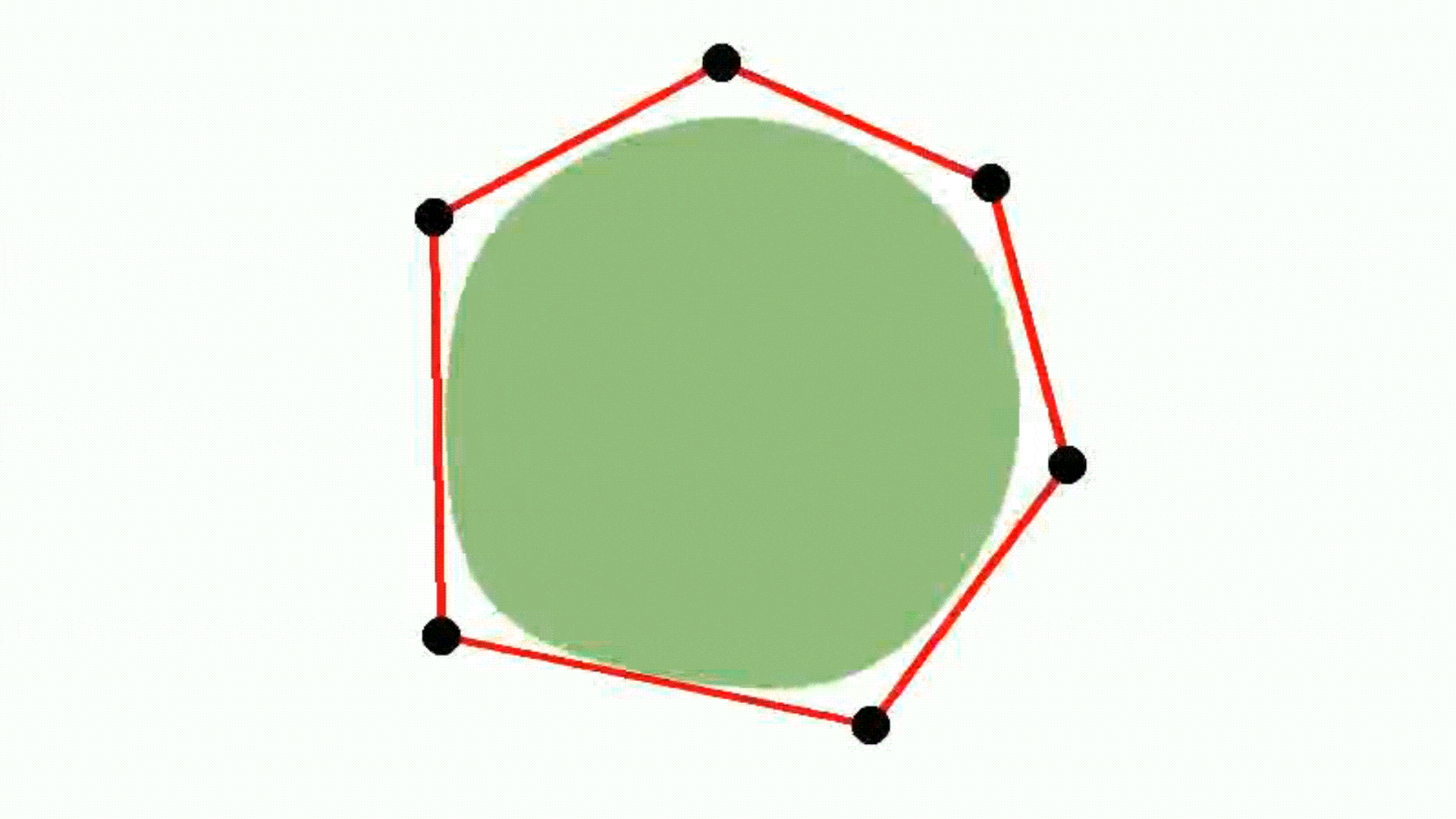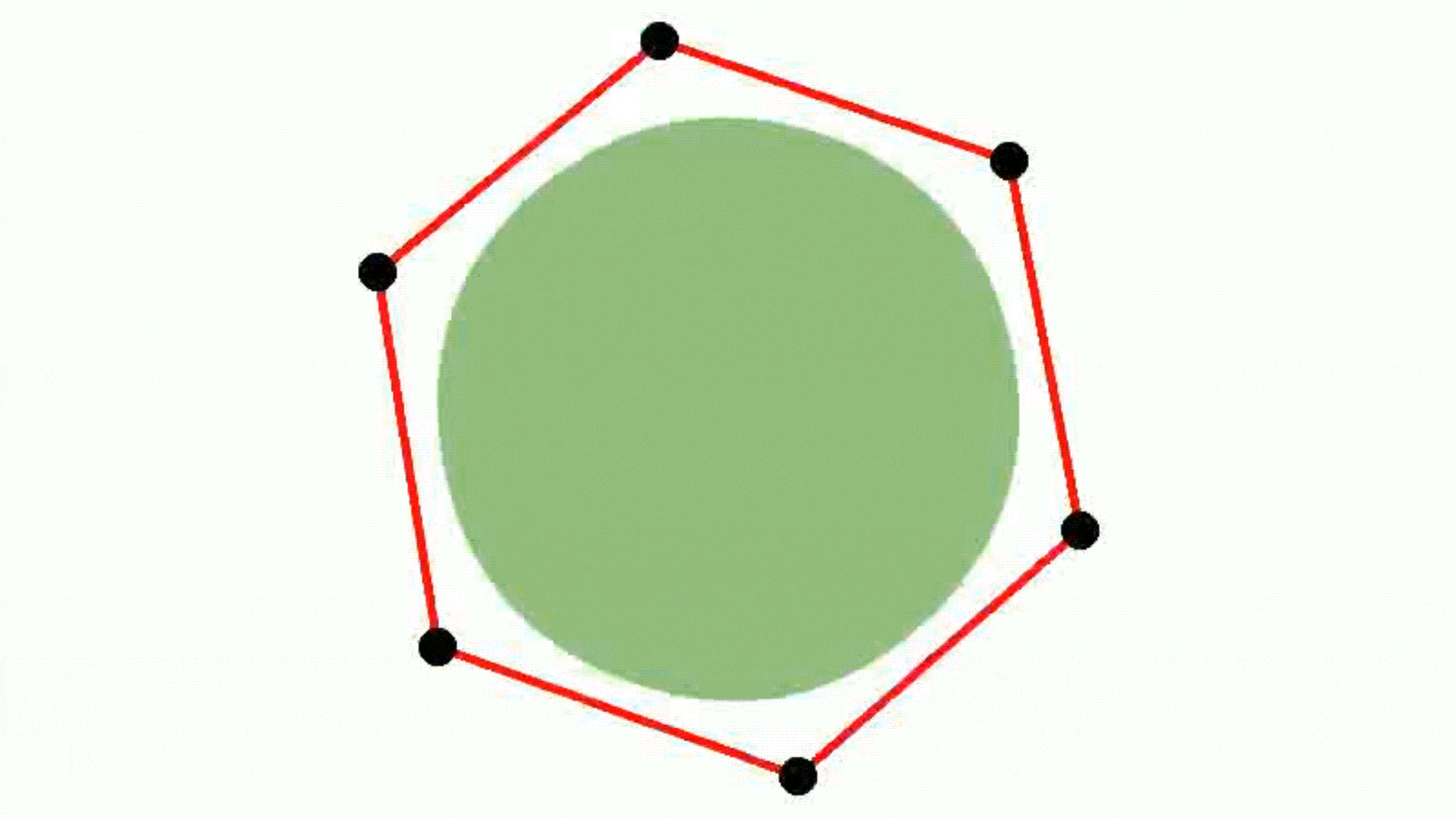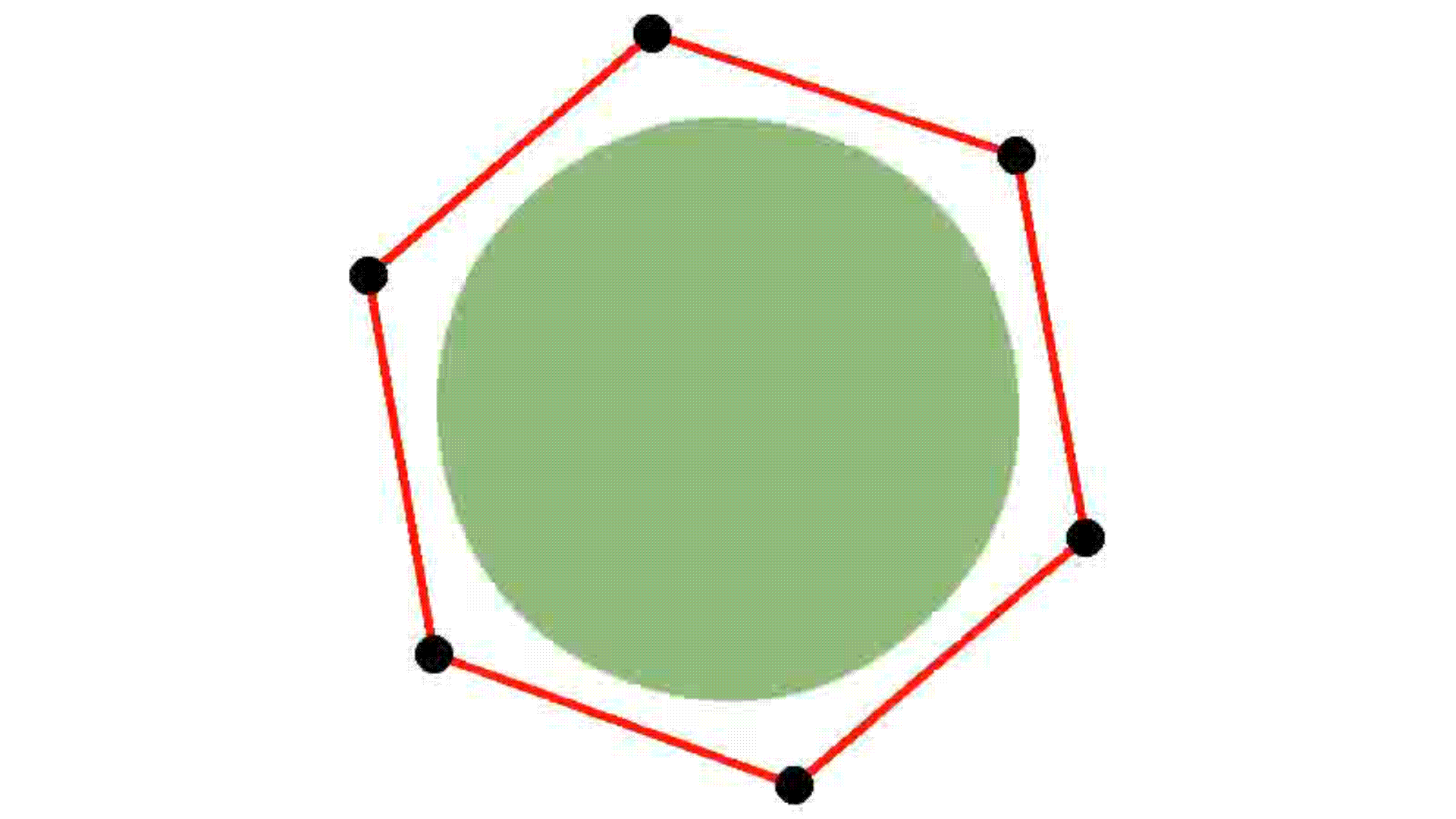
Circle
Isotropic Gaussian
Anisotropic Gaussian
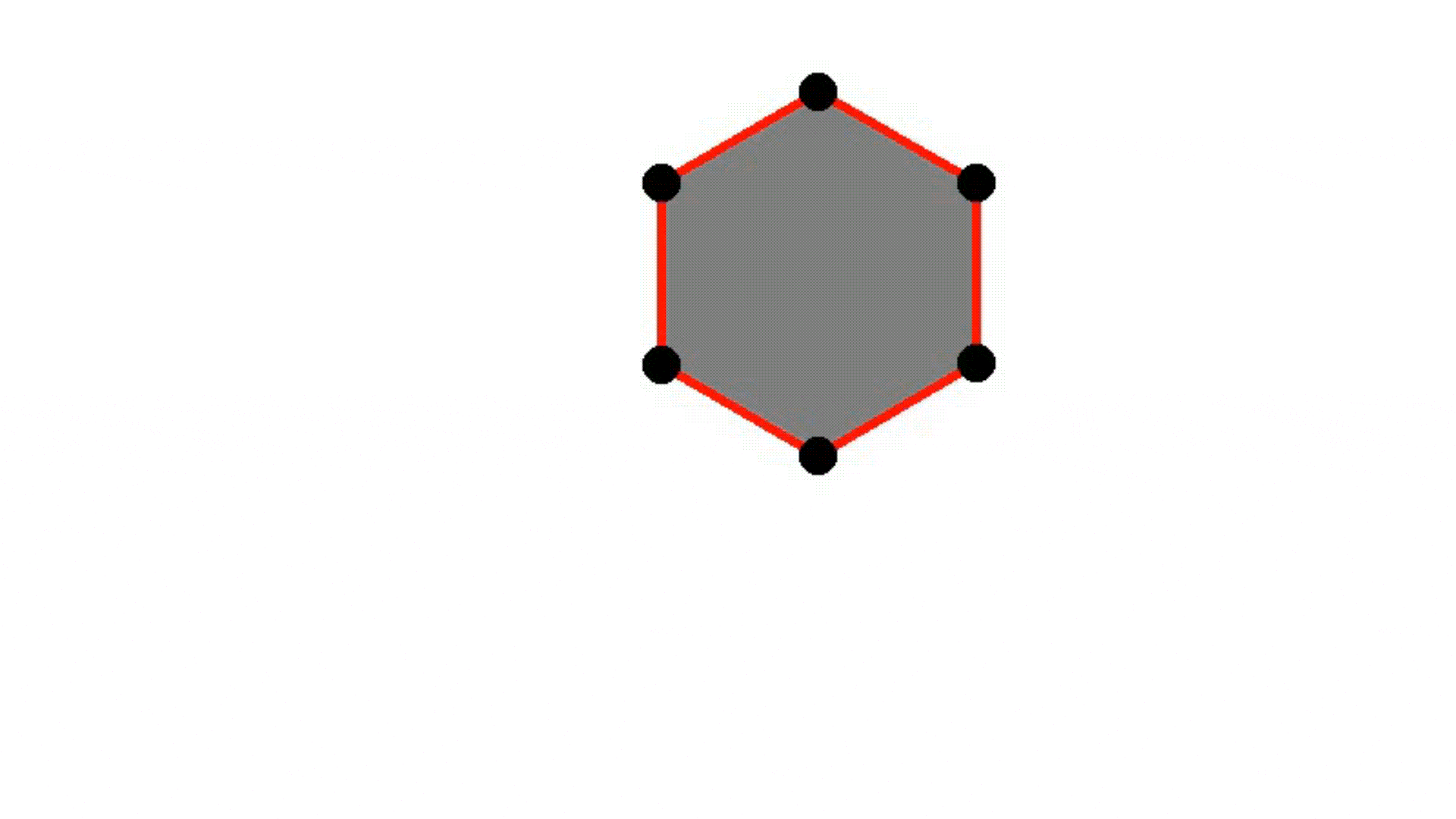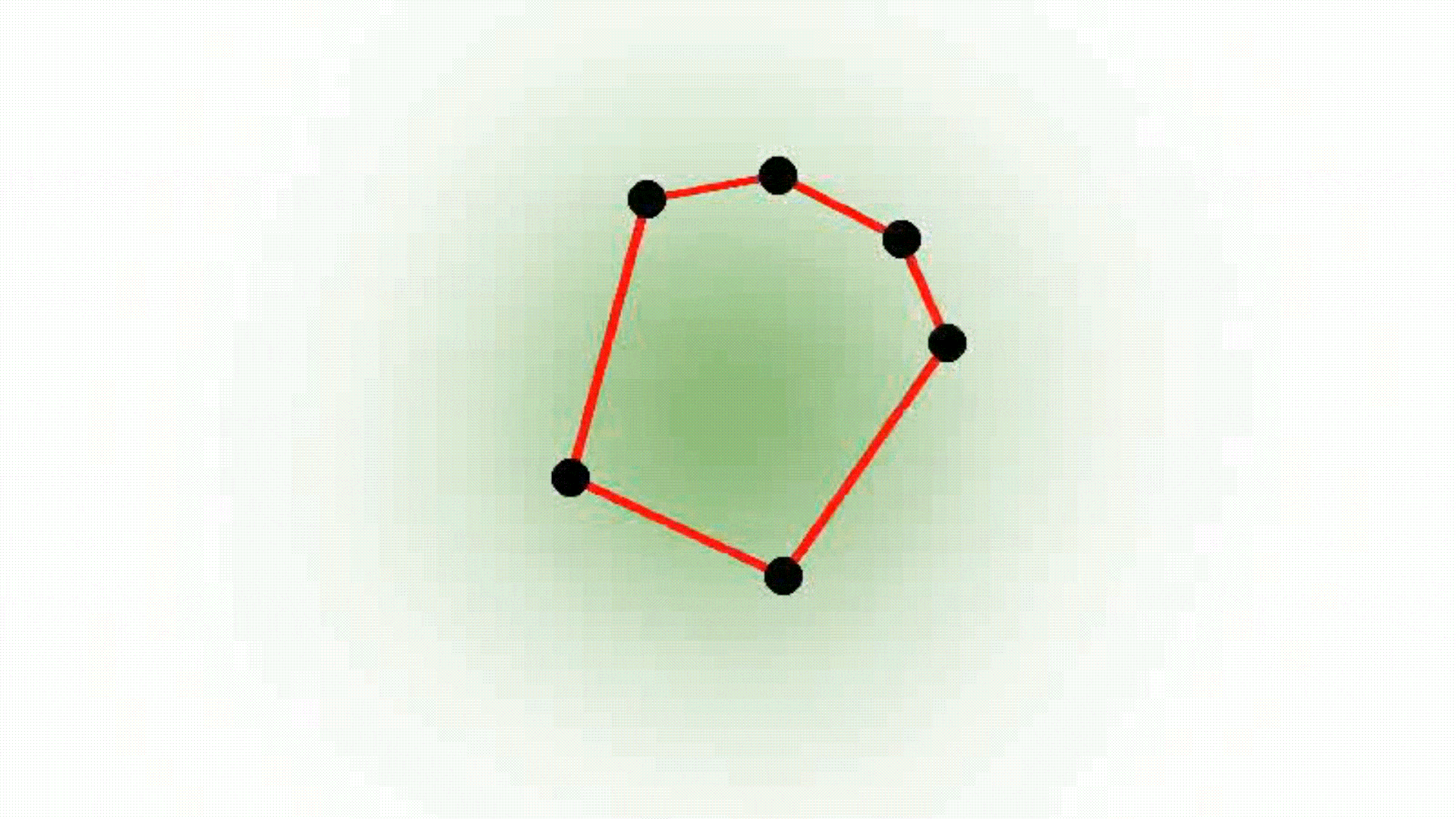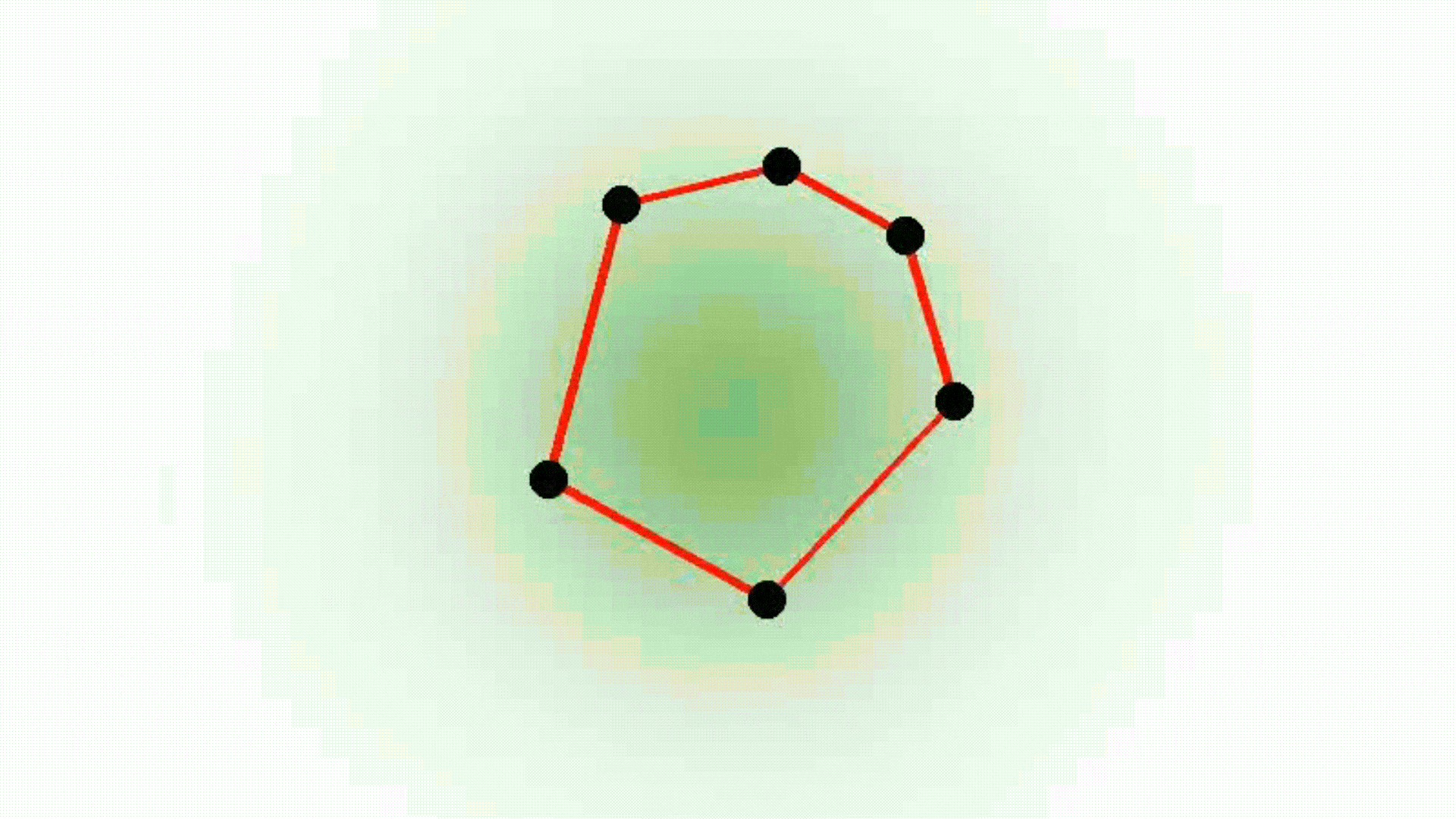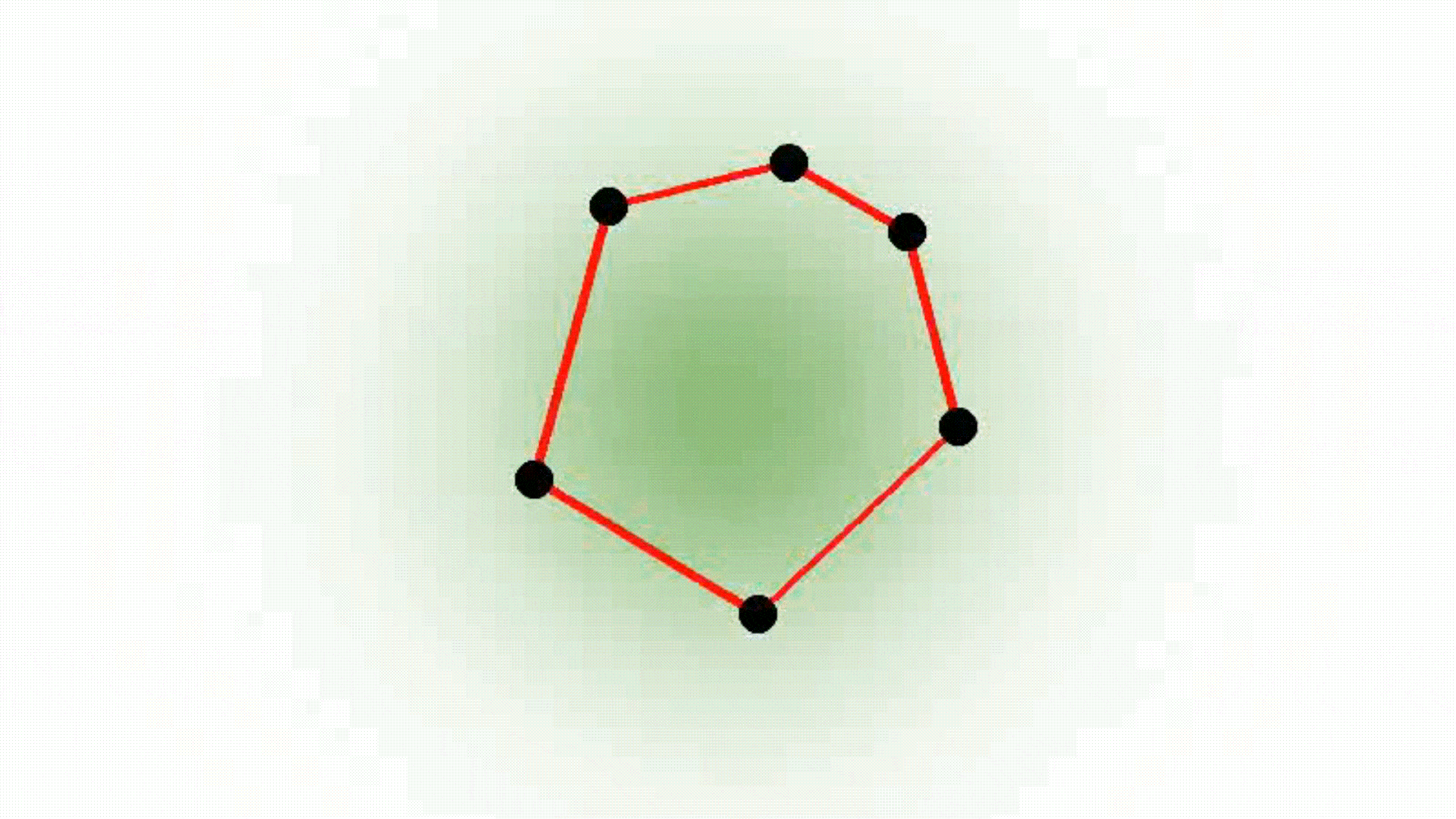
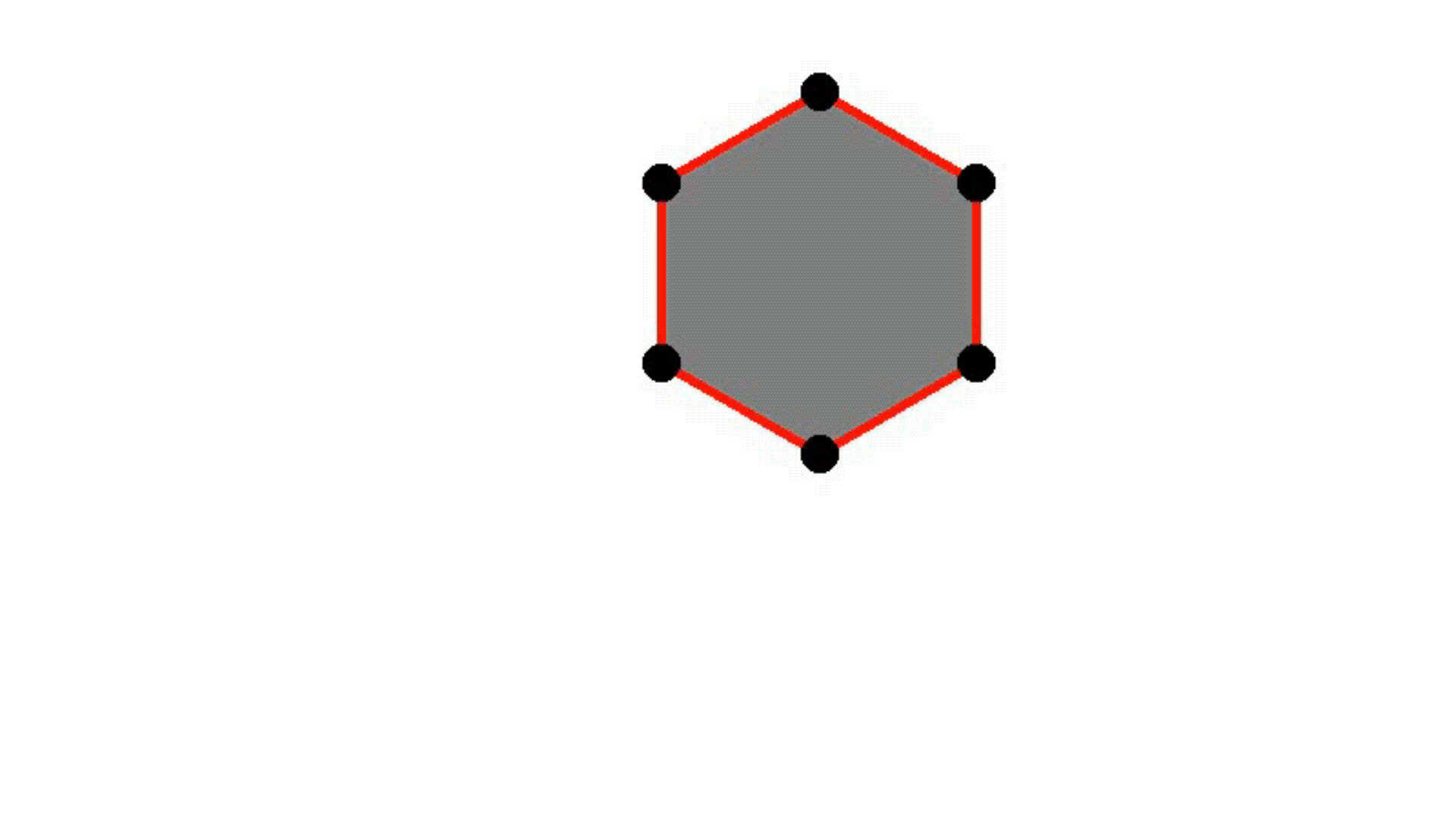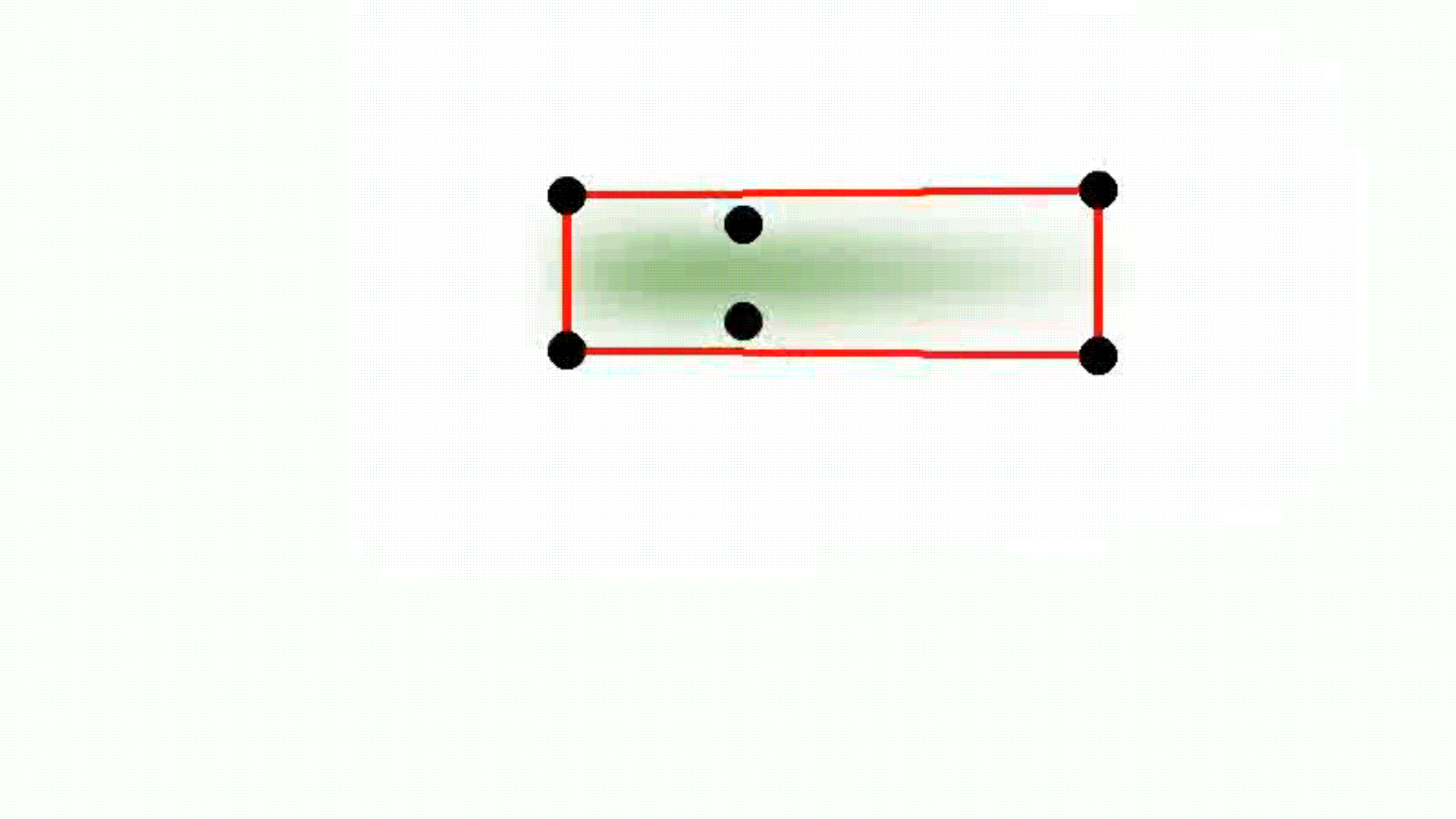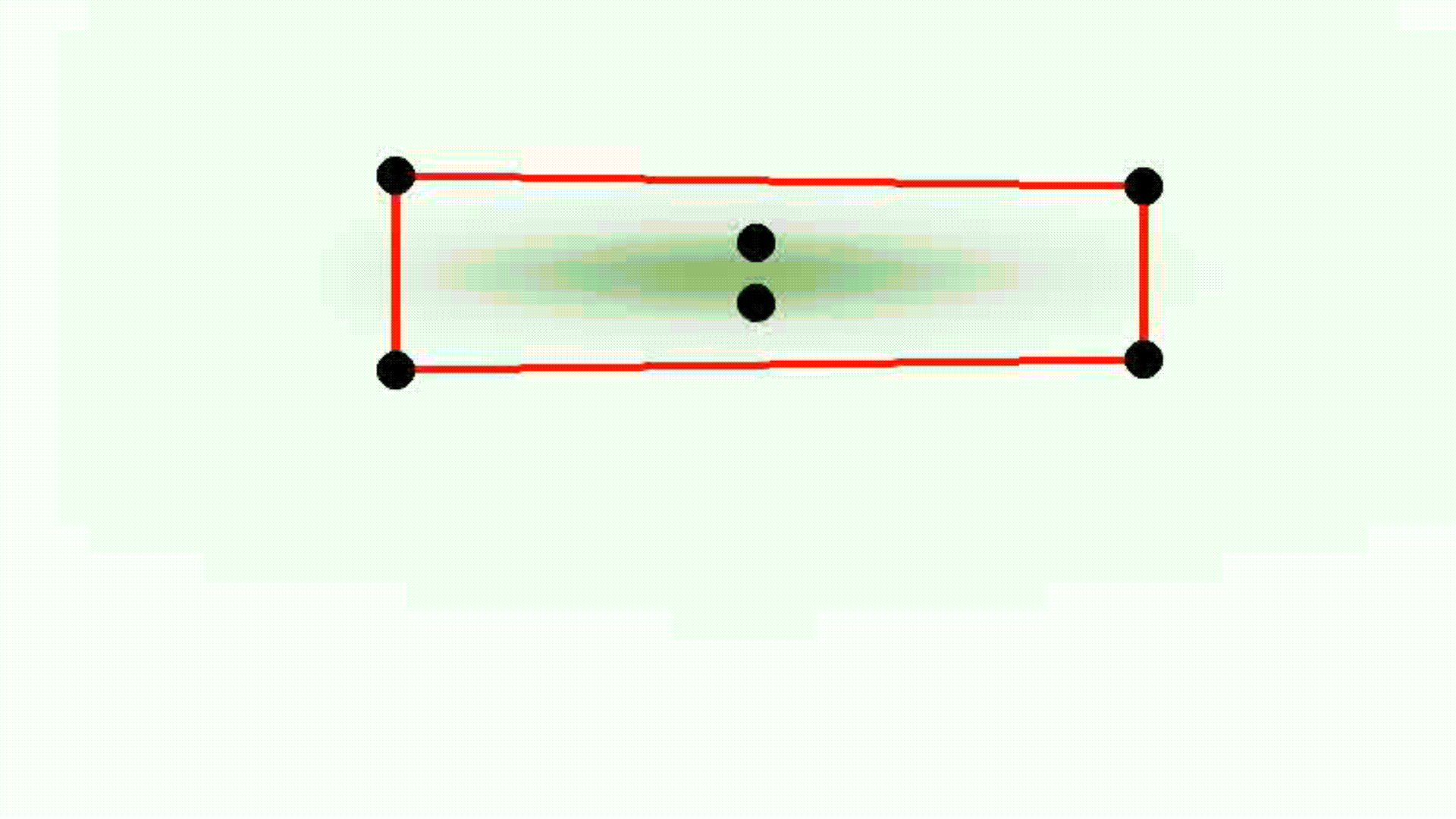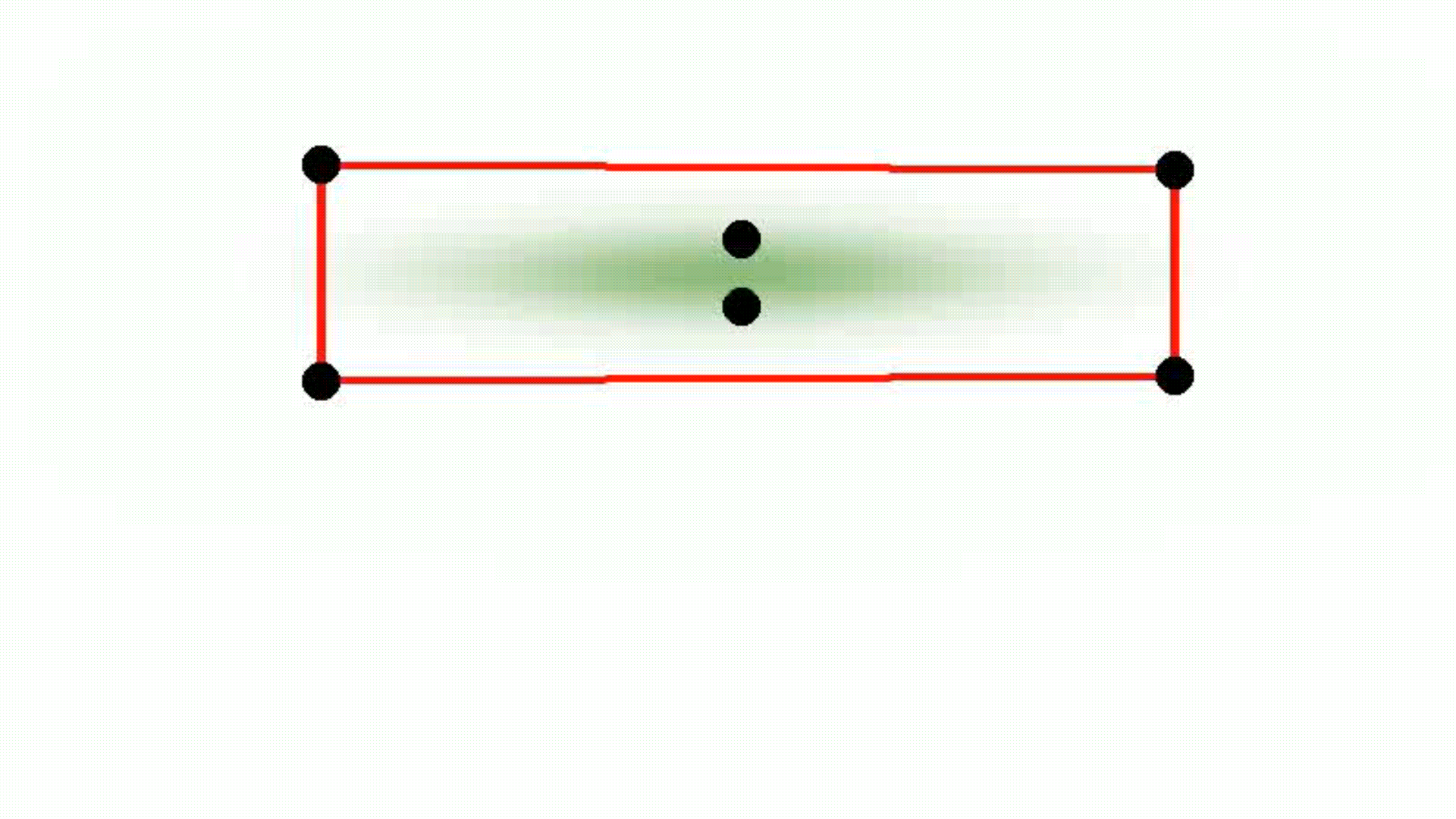
Smooth convexes can represent a wide variety of shapes, whether hard or soft, dense or diffuse, by varying the smoothness parameter δ and the sharpness parameter σ. They effectively approximate diverse geometries, including both polyhedra and Gaussians, while requiring fewer primitives for accurate representation. The red lines describe the convex hull, whereas the black dots represent the point set.
3D Convex Splatting produces sharper and more detailed images. Notably, it renders the road and flowers with greater realism and captures finer details compared to 3D Gaussian Splatting.
We render the truck scene with 10% and 50% of the final shapes to illustrate how the individual optimized 3D Smooth Convexes appear.
3D Convex Splatting consistently achieves higher rendering quality, outperforming other rendering primitives like 3D Gaussian Splatting (3DGS), 2D Gaussian Splatting (2DGS) and Generalized Exponential Splatting (GES). Meanwhile, the lightweight version uses 15% of the memory required by 3DGS while maintaining comparable rendering quality.
@article{Held20243DConvex,
title = {{3D} Convex Splatting: Radiance Field Rendering with {3D} Smooth Convexes},
author = {Held, Jan and Vandeghen, Renaud and Hamdi, Abdullah and Deli{`e}ge, Adrien and Cioppa, Anthony and Giancola, Silvio and Vedaldi, Andrea and Ghanem, Bernard and Van Droogenbroeck, Marc},
journal = {arXiv},
volume = {abs/2411.14974},
year = {2024},
eprint = {2411.14974},
eprinttype = {arXiv},
doi = {10.48550/arXiv.2411.14974},
url = {https://doi.org/10.48550/arXiv.2411.14974}
}